Keno - Detailed Mathematical Analysis

The version of Keno played in Maryland serves as a case study in the precise calculation of win probabilities and expected return—the latter referring to the result to be realized in the long run from each unit invested.

In Maryland, anyone may play keno at any of thousands of establishments that are wired with a television screen and an impossible-to-overlook, hot pink machine resembling a cash register. The player uses a pencil to complete a small slip; the attendant feeds the slip to the machine, which generates a computer-printed ticket that is protected from tampering via cryptographic checksum. Games—which are played every four minutes or so—can be viewed over the accompanying television monitor. The computer selects twenty numbers between one and eighty. The payout is calculated based upon how many numbers were chosen and how many were matched. Intriguingly, for the nine-spot and ten-spot games, there is a payout if the player fails to match any numbers—it obviously being an unusual event for zero of nine or ten selected numbers to match any of the twenty "dealt," so to speak, from the pool of eighty.

The probability that k of the n numbers chosen by the player, i.e.,

P_n(k)

occur in the twenty numbers chosen by the computer can straightforwardly be derived:

1. The number of possible outcomes equals the number of combinations of eighty numbers taken twenty at a time.

2. The number of ways in which k of the n numbers selected by the player occur in the twenty numbers selected (putatively at random) by the central Keno computer is equal to the number of ways in which k numbers can be chosen from a set of n numbers.

3. The number of ways in which the remainder of the numbers do not occur in the twenty numbers selected is given by the number of ways in which 20-k numbers can be chosen from a set of 80-n numbers.

Combining the foregoing, one finds that:

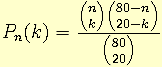
The payouts for each result can be read from the Maryland keno Web site. For the purposes of our discussion, if the player participates in the n-spot game and ends up matching k of the twenty numbers selected, we will refer to that payout as:

W_n(k)

The expected payout for the n-spot game can be determined by summing, over all values of i from one to n (from zero to n if the game pays out in the case of zero numbers matched), the product of the payout for that result and the probability of occurrence of that result:

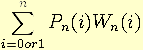
which could alternatively be represented as the inner product ("dot product") of the vector of probabilities and the vector of payouts.

One finds that the best game for the player is the three-spot game, which realizes an expected return of approximately 62 cents for every dollar invested, or approximately a 38% loss. The seven-spot game ranks close behind, returning just over 60 cents per dollar. Perhaps not surprisingly, despite the astonishingly high payoff for strong performance, the ten-spot game is by far the poorest from the player's perspective.

From Wikipedia's

Keno